Fourth circle theorem proof
You are here: Home
> Maths intro
> Circle theorems first page
> Cyclic quadrilateral proof
'Opposite angles in a cyclic quadrilateral add to 180°'
[A printable version of this page may be downloaded here.]
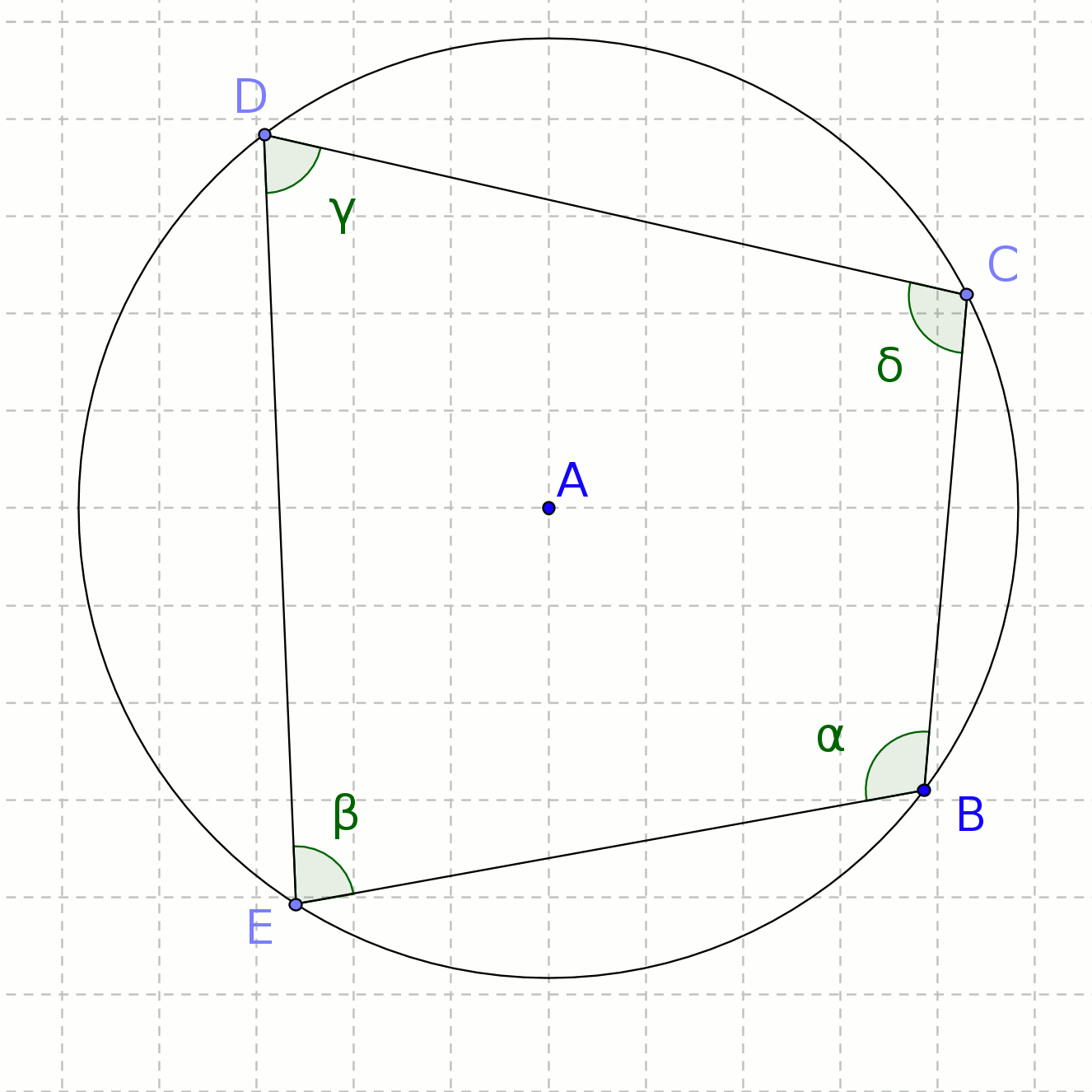
Fig 1
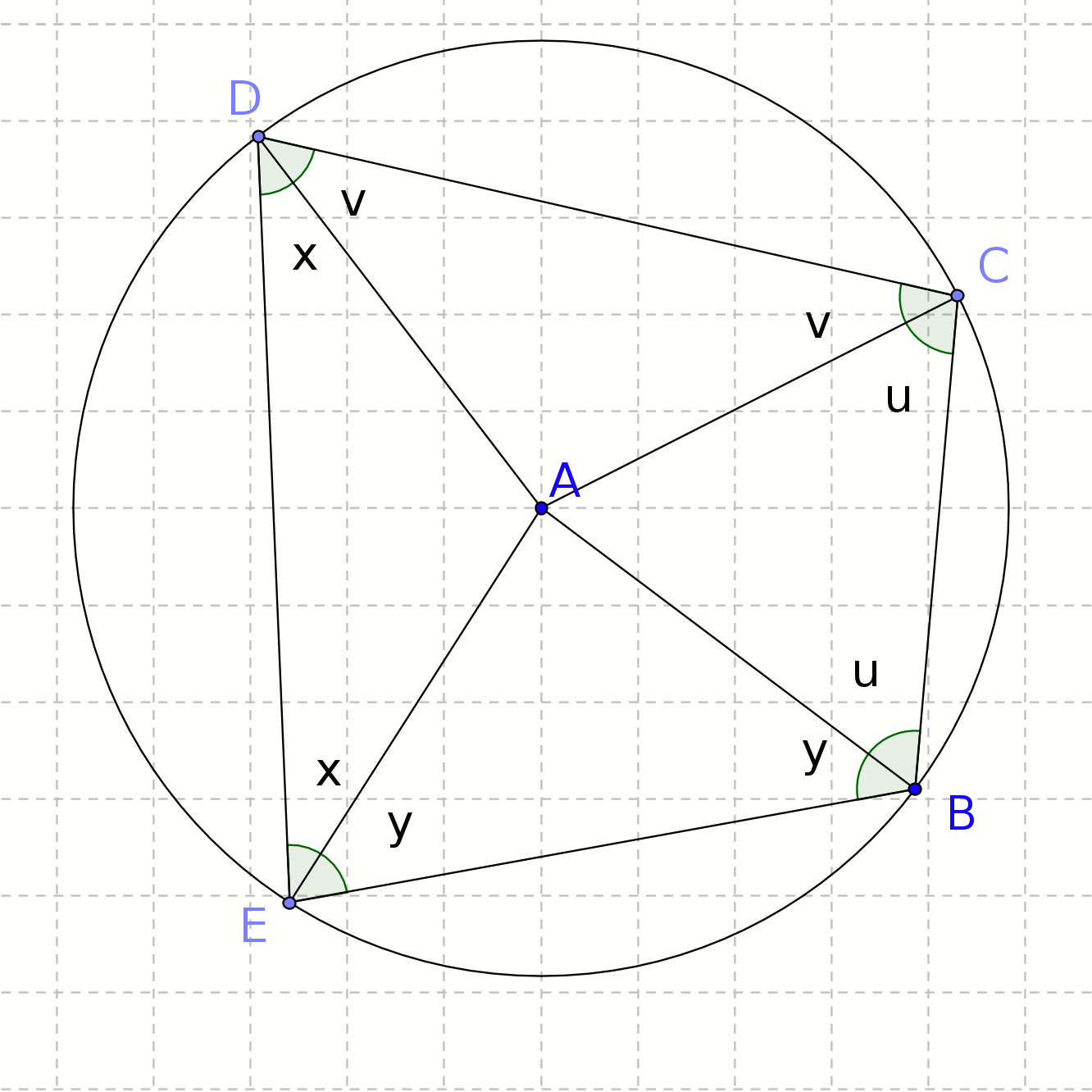
Fig 2
We need to show that for the angles of the cyclic quadrilateral, C + E = 180° = B + D (see fig 1)
('Cyclic quadrilateral' just means that all four vertices are on the
circumference of a circle.)
If you've looked at the proofs of the previous theorems, you'll expect the first step is to draw in radiuses from points on the circumference to the centre, and this is also the procedure here.
In the second diagram, fig 2, it is clear that the four triangles ABC, ACD, ADE and AEB are isosceles, as a pair of sides in each triangle are radiuses.
Thus the two angles in ABC marked 'u' are equal (and similarly for v, x and y in the other triangles.)
Now, B + C + D + E = 360° (sum of angles in a quadrilateral)
so (y+u) + (u+v) + (v+x) + (x+y) = 360°
2(u+v+x+y) = 360°
u+v+x+y = 180°
so C + E = (u+v) + (x+y) = 180° and
B + D = (y+u) + (v+x) = 180°
QED
|

