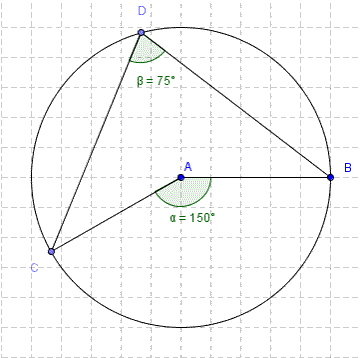
I'm calling CAB angle A, & CDB angle D, so we're going to prove that
A = 2D

















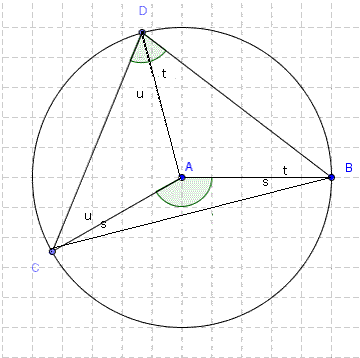
When you draw the radius AD and the chord CB, you get the diagram on the left, with three small triangles and one big one. The three triangles ABC, ADB & ACD are isoceles - as AB, AC & AD are radiuses (radii if you like;-)
So in each of these triangles, the two acute angles (s,t & u) in each are equal.

From the diagram, we can see D=t+u (i)
In triangle ABC, s+s+A = 180 (angles in triangle)
ie, A = 180-2s (ii)
In triangle BCD, (t+s) + (s+u) + (u+t) = 180 (angles in triangle again)
so 2s+2t+2u = 180
ie 2t+2u = 180-2s (iii)

so A = 2t+2u = 2D from (i),(ii) & (iii)

We've shown that
'the angle at the centre is twice the angle at the circumference'.

QED